Answer:
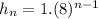 will be the correct formula for the given sequence.
will be the correct formula for the given sequence.
Explanation:
The given sequence is 1, 8, 64, 512...........
The given sequence is a geometric sequence having a common ratio (r) of
r =
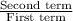
r =
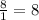
Since explicit formula of a geometric sequence is given by
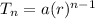
where
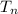 = nth term of the sequence
= nth term of the sequence
a = first term of the sequence
r = common ratio of the successive term to the previous term
Now we plug values of a and r in the formula to get the explicit formula for the given sequence.
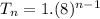
Therefore, if Bernardo is saying that the formula of the sequence is
h(n) =
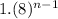 then he is correct.
then he is correct.