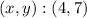Question

Solve the following system:

y = x + 3
3x + y = 19
(7,4)
(-4,7)
(4,7)
(4,-7)

Answer 1

For this case we have the following system of equations:

`y = x + 3\\3x + y = 19`

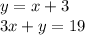
We solve by the substitution method:

We substitute the first equation in the second equation:

`3x + x + 3 = 19`

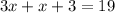
We add similar terms:

`4x + 3 = 19`

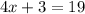
We subtract 3 from both sides of the equation:

`4x = 19-3\\4x = 16`

We divide between 4 on both sides of the equation:

`x = \frac {16} {4}\\x = 4`

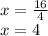
We look for the value of the variable y:

`y=x+3\\y=4+3\\y=7`

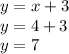
Finally, the solution of the system is:

`(x, y) :( 4,7)`

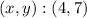
Answer:

`(x, y) :( 4,7)`