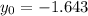Question

Find the value of y0 for which the solution touches, but does not cross, the t-axis. (a computer algebra system is recommended. round your answer to three decimal places.)

Answer 1

`y_0 = -1.643`

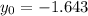
Explanation:

Assuming the following function:

`y' + (2)/(3)y = 1-(1)/(2)t , y(0)=y_0`

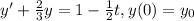
So we want to find a point a such that:

`y(a) = 0 , y'(a) =0 , y''(a) \\eq 0`

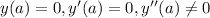
So if we use this condition we can find the value of t=a that satisfy the equirements:

`0 +(2)/(3) 0 = 1- (1)/(2)a`

`a=2`

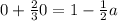
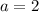
And we have another initial conidtion
`y(2)=0, y'(2)=0`

Now we need to solve the differential equation and since is a linear equation we can use the integrating factor, our equation have the following form:

`y'(x) + p(x) y = q(x)`

`p(x) = (2)/(3), q(x) = 1-(t)/(2)`

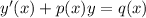
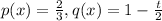
We can calculate the integrating factor like this:

`\mu(t) = e^{\int (2)/(3)dt} =e^{(2t)/(3)}`

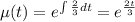
Now we can rewrite the differential equation like this:

`[e^{(2t)/(3)}y]' = e^{(2t)/(3)}-(e^(2t/3))/(2)t`

And if we integrate both sides we got this:

`ye^{(2t)/(3)}= (3)/(2)e^{(2t)/(3)}-(1)/(2) [(3)/(2)te^{(2t)/(3)}-(9)/(4)e^{(2t)/(3)}]+C`

If we divide both sides by
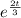`e^{(2t)/(3)}` we got this:

`y = (21)/(8) -(3)/(4) t +Ce^{-(2t)/(3)}`

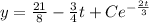
And we can use the initial condition
`y(0)=y_0` and we find the value for C like this:

`C = y_0 - (21)/(8)`

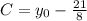
And then we have our solution given by:

`y =(21)/(8) -(3)/(4)t +(y_0 -(21)/(8))e^{-(2t)/(3)}`

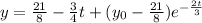
And if we use the other initial condition
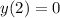`y(2) =0` w can solve the value of
`y_0`

`0 =(21)/(8) -(3)/(4)2 +(y_0 -(21)/(8))e^{-(4)/(3)}`

`y_0 = \frac{(21)/(8) (e^{-(4)/(3)} -1)+ (3)/(2)}{e^{-(4)/(3)}}=-1.643`

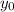
And then that would be our final solution:

`y_0 = -1.643`