Answer:
After 1023.4 years the mass of the substance will be 30 g.
Step-by-step explanation:
Hi there!
Let´s write the function (according to what I found on the web):
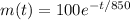
We have to find the time "t1" at which the mass of the substance is 30 g. Mathematically:
m(t1) = 30
Then:
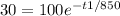
Let´s solve the equation for t1. First, divide by 100 both sides of the equation:
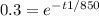 [/tex]
[/tex]
Apply ln to both sides of the equation:
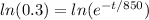
Use the logarithm property: ln (aᵇ) = b ln(a)
ln(0.3) = -t/850 · ln (e) (ln (e) = 1)
ln(0.3) = -t/850
850 ln(0.3) = -t
t = -850 ln(0.3)
t = 1023.4
After 1023.4 years the mass of the substance will be 30 g.