Question

Machine A and Machine B can produce 1 widget in 3 hours working together at their respective constant rates. If Machine A's speed were doubled, the two machines could produce 1 widget in 2 hours working together at their respective rates. How many hours does it currently take Machine A to produce 1 widget on its own?

Answer 1

Machine A take 6 hours to produce 1 widget on its own.

Explanation:

Consider the provided information.

Machine A and Machine B can produce 1 widget in 3 hours working together at their respective constant rates.

Let Machine A takes 'x' hours to produce 1 widget.

Thus, in every hour it will produce
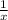`(1)/(x)` th of widget.

Similarly Machine B takes 'y' hours to produce 1 widget.

In every hour it will produce
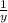`(1)/(y)` th of widget.

If both machine work together they can produce 1 widget in 3 hrs.

Therefore, work done by A and B together in 1 hour is:

`(1)/(3) =(1)/(x)+(1)/(y)` ......(1)

If Machine A's speed were doubled, the two machines could produce 1 widget in 2 hours working together at their respective rates.

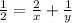`(1)/(2) =(2)/(x)+(1)/(y)` ......(2)

Subtract equation 1 from equation 2.

`(1)/(2)-(1)/(3)=(2)/(x)-(1)/(x)+(1)/(y)-(1)/(y)`

`(3-2)/(6)=(2-1)/(x)`

`(1)/(6)=(1)/(x)`

`x=6`

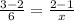
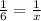
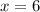
Hence, machine A take 6 hours to produce 1 widget on its own.