Question

How do you reconcile the law of falling bodies (that all objects fall to earth at the same acceleration despite their weight) with the Second Law of Motion which states that the acceleration of a body subjected to an applied force is inversely proportional to its mass?

Answer 1

From the gravity acceleration theorem due to a celestial body or planet, we have that the Force is given as

`F = \frac {GMm} {r ^ 2}`

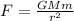
Where,

F = Strength

G = Universal acceleration constant

M = Mass of the planet

m = body mass

r = Distance between centers of gravity

The acceleration by gravity would be given under the relationship

`g = \frac {F} {m}`

`g = \frac {GM} {r ^ 2}`

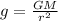
Here the acceleration is independent of the mass of the body m. This is because the force itself depended on the mass of the object.

On the other hand, the acceleration of Newton's second law states that

`a = \frac {F} {m}`

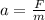
Where the acceleration is inversely proportional to the mass but the Force does not depend explicitly on the mass of the object (Like the other case) and therefore the term of the mass must not necessarily be canceled but instead, considered.