Question

Suppose that S is the set of successful students in a classroom, and that F stands for the set of freshmen students in that classroom.

Find n(S ∩ F) given that n(S) = 54, n(F) = 28 and n(S ∪ F) = 58a) 112b) 24c) 82d) 0e) 140

Answer 1

b) 24

Explanation:

We solve building the Venn's diagram of these sets.

We have that n(S) is the number of succesful students in a classroom.

n(F) is the number of freshmen student in that classroom.

We have that:

`n(S) = n(s) + n(S \cap F)`

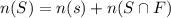
In which n(s) are those who are succeful but not freshmen and
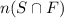`n(S \cap F)` are those who are succesful and freshmen.

By the same logic, we also have that:

`n(F) = n(f) + n(S \cap F)`

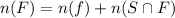
The union is:

`n(S \cup F) = n(s) + n(f) + n(S \cap F)`

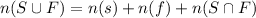
In which

`n(S \cup F) = 58`

`n(s) = n(S) - n(S \cap F) = 54 - n(S \cap F)`

`n(f) = n(F) - n(S \cap F) = 28 - n(S \cap F)`

So

`n(S \cup F) = n(s) + n(f) + n(S \cap F)`

`58 = 54 - n(S \cap F) + 28 - n(S \cap F) + n(S \cap F)`

`n(S \cap F) = 24`

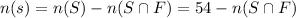
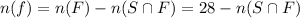
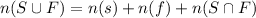
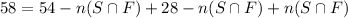
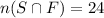
So the correct answer is:

b) 24