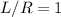Answer:
a) it has been shown
b)
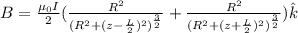
c) it has been shown
d)
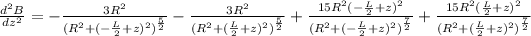
e)
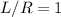
Step-by-step explanation:
a)
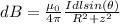 where
where
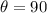 °
°
Then,
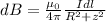
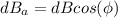 where
where
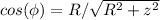
Then,

So total magnetic field can be found as follows,
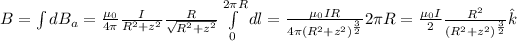
b) Since the first loop is L/2 distance above center, when we choose arbitrary point at z-axis, the distance will be z - L/2. Also, since the second loop is L/2 below the center, same arbitrary point's distance from the loop will be z + L/2. Moreover, since the position of loops is symmetric, choosing arbitrary point from anywhere will not change the result. So now, let's write the above equation down with corresponding consideration.
Since there are 2 loops, their magnetic fields will be added to each other to find the total magnetic field.
Thus,
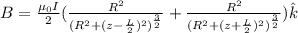
c) The derivative of the equation in part (a) will be as follows,
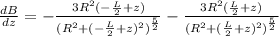
At
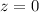 , the above equation becomes as follows,
, the above equation becomes as follows,
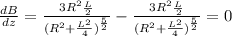
d) The second derivative of the equation in part (a) will be as follows,
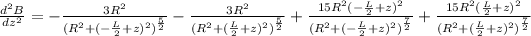
e) At
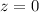 , the above equation becomes as follows,
, the above equation becomes as follows,
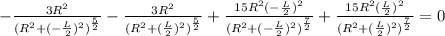
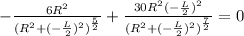
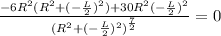
The denominator cannot be equal to zero.
Hence,
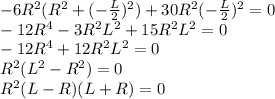
The solutions are
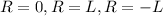 . However
. However
 and
and
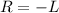 cannot be possible.
cannot be possible.
So the result is
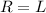
Thus,