Answer: b) 100
Explanation:
Given : Number of senior partners =4
Number of junior partners. = 6
Total partners = 4+ 6= 10
Total Number of ways to choose 3 partners
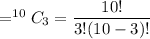
![[\because\ ^nC_r=(n!)/(r!(n-r)!)]](https://img.qammunity.org/2021/formulas/mathematics/high-school/zrmo4r4y9f0jf5snvf5g7y7vn0g3983fd8.png)

i.e. Total Number of ways to choose 3 partners =120
The number of ways that none of 3 partners are seniors =tex]=^{6}C_3=\dfrac{6!}{3!(6-3)!}=20[/tex]
Now , the different groups of 3 partners can be formed in which at least one member of the group is a senior partner
= Total Number of ways to choose 3 partners- Number of ways that none of 3 partners are seniors
= 120-20=100
Hence, the correct answer is b) 100.