Question

A rectangle or box has a perimeter of 76 inches. If two of the boxes are placed next to each other on the long side the new box is a rectangle shape but the perimeter of 112 inches .

What are the dimensions of the original rectangle ?

Answer 1

The dimension of the rectangle

Length = 20 inches

Breadth = 18 inches

Explanation:

Given:

The perimeter of rectangle = 76 inches

Perimeter of the newly formed rectangle = 112 inches

To Find:

Dimensions of the original rectangle = ?

Solution:

The perimeter rectangle

=> 2(L+B) =76 inches -----------------------(1)

If two of the boxes are placed next to each other on the long side the new box is a rectangle shape is formed

Then the perimeter of the new rectangle box will be

=> 2(L+B) + 2(L+B) - 2L = 112--------------------(2)

Substituting (1) in(2)

=> 76+ 76 - 2L = 112

=>156 -2L =112

=>2L = 156 -112

=> 2L = 40

=> L=
`(40)/(2)`

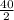
=>L = 20

Substituting L =20 in eq(1)

=> 2(20+B) =76

=> (40 +2B) = 76

=>2B = 76-40

=> 2B =36

=> B =
`\frac {36}{2}`

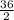
=> B = 18