The line contains (9,y) and (-6,3) Then y is 13
Solution:
Given that a line contains (9, y) and (-6, 3)
Slope of line is

To find: y
The slope of line is given as:
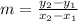
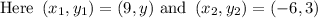
Substituting the values in formula,
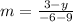
Substitute
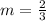
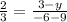
2(-6 - 9) = 3(3 - y)
Multiplying the terms with terms inside bracket
-12 - 18 = 9 - 3y
Move the variable to one side
-30 = 9 - 3y
On solving we get,
3y = 30 + 9
3y = 39
Divide both sides by 3, we get
y = 13
Thus y = 13