Question

Jaxon and Robert go the movie theater and purchase refreshments for their friends. Jaxon spends a total of $71.75 on 2 drinks and 9 bags of popcorn. Robert spends a total of $ 143.00 on 12 drinks and 8 bags of popcorn. Write a system of equations that can be used to find the price of one drink and the price one bag of popcorn. Using these equations, determine, and state the price of a drink, to the nearest cent.

Answer 1

Explanation:

Answer 2

The system of equations are
`\left \{ {{2x+9y=71.75} \atop {12x+8y=143}} \right.`

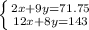
The price of one drink is $7.75 and the price one bag of popcorn is $6.25.

Explanation:

Let the cost of 1 drink be 'x'.

And also let the cost of 1 bag of popcorn be 'y'.

Now according to question,

Jaxon spends a total of $71.75 on 2 drinks and 9 bags of popcorn.

So framing in equation form, we get;

`2x+9y=71.75\ \ \ \ \ equation\ 1`

Again, Robert spends a total of $ 143.00 on 12 drinks and 8 bags of popcorn.

So framing in equation form, we get;

`12x+8y=143\ \ \ \ \ equation\ 2`

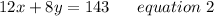
Multiplying equation 1 with 6 we get;

`6(2x+9y)=6*71.75\\\\12x+54y = 430.5`

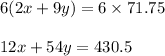
Now Subtracting equation 2 from equation 1 we get;

`(12x+54y) -(12x+8y) = 430.5-143\\\\12x+54y-12x-8y= 287.5\\\\46y= 287.5\\\\y=(287.5)/(46)= \$6.25`

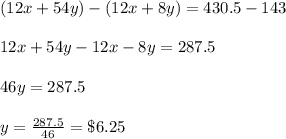
Now Substituting the value of y in equation 1 we get;

`2x+9y=71.75\\\\2x+9*6.25 =71.75\\\\2x+56.25=71.75\\\\2x=71.75-56.25\\\\2x=15.5\\\\x=(15.5)/(2) =\$7.75`

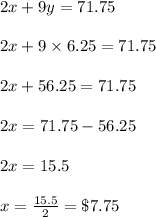
Hence The system of equations are
`\left \{ {{2x+9y=71.75} \atop {12x+8y=143}} \right.`

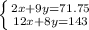
Also The price of one drink is $7.75 and the price one bag of popcorn is $6.25.