Question

A function f(x) has x intercepts of -3 and -5. What is the constant term in the function?

F(x)=x^2+8x+

Answer 1

The constant term in the function is 5

Explanation:

we have

`f(x)=x^(2)+8x+b`

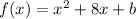
where

b is the y-intercept or the constant term of the function

Remember that

The x-intercept is the value of x when the value of the function is equal to zero

so

For x=-3 ----> f(x)=0

For x=-5 ----> f(x)=0

substitute any of the intercepts in the function

For x=-3

`0=(-3)^(2)+8(-3)+b`

`0=9-24+b`

`0=-15+b`

`b=15`

`f(x)=x^(2)+8x+15`

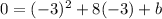
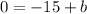
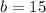
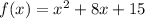
Verify with the other intercept

For x=-5

`0=(-5)^(2)+8(-5)+15`

`0=25-40+15`

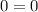`0=0` ---> is true

therefore

The constant term in the function is 5