Question:
A geometric sequence is defined by the equation an = (3)^3 − n. What are the first three terms of the sequence and what is the common ratio, r?
Answer:
The first three terms of sequence is 9, 3 , 1
The common ratio is

Solution:
The geometric sequence is defined by the equation:
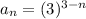
To find the first three terms of sequence, substitute n = 1, n = 2, n = 3
First term:
Put n = 1 in given equation
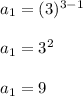
Thus first term of sequence is 9
Second term:
Put n = 2 in given equation
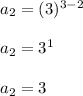
Thus second term of sequence is 3
Third term:
Put n = 3 in given sequence
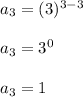
Thus third term of sequence is 1
Thus the first three terms of sequence is 9, 3 , 1
To find common ratio:
Common ratio is found by dividing the two consecutive terms
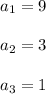
Thus common ratio is obtained as:
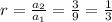
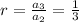
Thus common ratio is
