Question

A block of mass 5 kg is placed on a rough table having a coefficient of static friction μs = 0.2.What is the force required to move the block?

Answer 1

We need to (at least) apply a force of 9.8 N to move the block

Step-by-step explanation:

Second Newton's Law

If a net force
`F_n` different from zero is applied to an object of mass m, then it will move at an acceleration a, given by

`F_n=ma`

If we apply a force F to an object placed on a rough surface, the only way to make it move is to beat the friction force which is given by

`F_r=\mu F_N`

Where
`\mu` is the static friction coefficient and
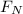`F_N` is the normal force exerted by the table to the object. Since there is no motion in the vertical direction the normal force equals the weight of the object:

`F_N=mg=5\ kg\ 9.8\ m/s^2=49\ N`

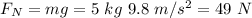
The friction force is

`F_r=0.2 (49)=9.8\ N`

Thus, we need to (at least) apply a force of 9.8 N to move the block