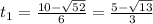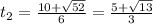Answer:
a)
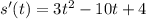
b)
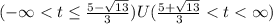
c)
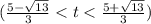
d)
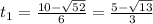
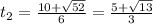
Step-by-step explanation:
We have the following parts:
(a) find the velocity function of the particle at any time t ≥0 )
For this case w ejust need to take the derivate of s(t) and we got:
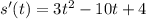
(b) identify the time interval(s) in which the particle is moving in a positive direction
The partcile is moving in the positive direction when the velocity is higher than 0. We have a quadratic equation for the velocity so we can solve for the t intercepts like this:
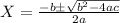
For this case
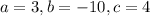
And if we replace we got:

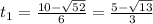
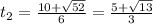
And now we can see on which intervals we have the velocity positive or negative:
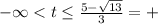

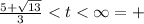
So the is positive between
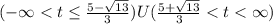
(c) identify the time interval(s) in which the particle is moving in a negative direction
From the before part we see that the velocity is negative just on this interval:
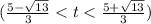
(d) identify the time(s) at which the particle changes direction. s(t) = t³ - 5t²+4t
The points where the particle changes direction are given by the critical point because are the points where the derivate is 0 and we have the change of direction and on this case are: