Question

Determine the approximate value of θ. (Plz no wrong answers, it's not 52.1)

Group of Answers:

38.9

51.1

37.9

52.1

Answer 1

Explanation:

`sin \theta=(7)/(9)\\\theta=sin^(-1) ((7)/(9))\\\approx~ 51.1 ^\circ`

Answer 2

Answer: 51.1

Explanation:

In the given picture , we have a right triangle Δ DEF right-angled at ∠F i.e. ∠ F= 90°.

Hypotenuse = DE = 9 units (Side opposite to right angle is hypotenuse)

`\angle{E}=\theta`

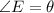
and FD = 7 units

According to the trigonometry in a right triangle ,

`\sin x=\frac{\text{Side opposite to x}}{\text{Hypotenuse}}`

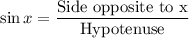
In Δ DEF

So ,
`\sin\theta=(FD)/(DE)`

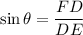
[tex]\sin\theta=\dfrac{7}{9}\\\\ theta =\sin^{-1}(\dfrac{7}{9})\\\\=51.05755873\approx 51.1\ \ [\text{By using sin calculator.}]/tex]

Hence, the approximate value of θ is 51.1.

So the correct answer is "51.1".