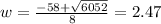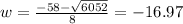Question

Suzanne has a rectangular garden which is 18 feet long and 11 feet wide. She has 168 square foot of paving stones, and she wants to build a pathway around the border of the garden. How wide will the pathway be?

Answer 1

width = 2.5 feet

Explanation:

Suzanne has a rectangular garden which is 18 feet long and 11 feet wide.

Area of the garden = length times width = 18 times 11= 198 square foot

Let 'w' be the width of the border

Length of the garden with border = 18+2w

Width of the garden with border = 11+2w

Area of the garden with border =
`(18+2w)(11+2w)=4w^2+58w+198`

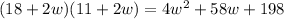
Area of the border =
`4w^2+58w+198-198=4w^2+58w`

She has 168 square foot of paving stones,

`4w^2+58w=168`

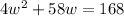
Solve for w

apply quadratic formula

a= 4, b= 58 and c=-168

`\quad x=(-b\pm √(b^2-4ac))/(2a)`

`w=(-58+-√(58^2-4\cdot \:4\left(-168\right)))/(2\cdot \:4)`

`w=(-58+-√(6052))/(8)`

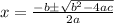
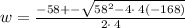
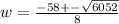
we get two values for w

`w=(-58+√(6052))/(8)=2.47`

`w=(-58-√(6052))/(8)=-16.97`