Answer:
1) The option
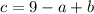 is correct.
is correct.
2) The option x=-2 or x=-3 is correct.
3) The option
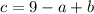 is correct.
is correct.
4) The option
 is correct.
is correct.
5) The option x=-2 or x=-3 is correct.
Explanation:
1) Given equation is

Now to solve the equation for c:

Squaring on both sides we get
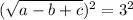

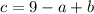
Therefore the option
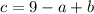 is correct.
is correct.
2) Given equation is
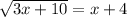
Now to solve the equation for x:
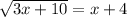
Squaring on both sides we get

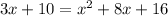
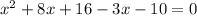
 which is a quadratic equation in x.
which is a quadratic equation in x.
We can solve it by finding factors
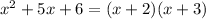
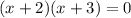
x+2=0 or x+3=0
Therefore x=-2 or x=-3
Therefore the option x=-2 or x=-3 is correct.
3) Given equation is

Now to solve the equation for c:

Squaring on both sides we get
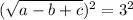

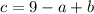
Therefore the option
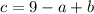 is correct.
is correct.
4) Given equation is
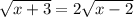
Now to solve the equation for x:
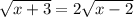
Squaring on both sides we get

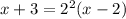
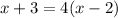
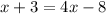
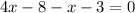
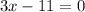

Therefore the option
 is correct.
is correct.
5) Given equation is
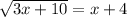
Now to solve the equation for x:
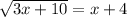
Squaring on both sides we get

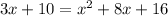
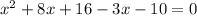
 which is a quadratic equation in x.
which is a quadratic equation in x.
We can solve it by finding factors
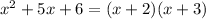
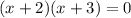
x+2=0 or x+3=0
Therefore x=-2 or x=-3
Therefore the option x=-2 or x=-3 is correct.