Question

The load required to cause buckling depends on how the column is attached to its supports. The maximum or critical load for a column of length L that is pin supported at both ends is Pcr=?2EIL2.

Part A - Maximum load

A column is made from a rectangular bar whose cross section is 5.3 cm by 9.6 cm . If the height of the column is 2 m , what is the maximum load it can support? The material has E = 200 GPa and ?Y = 250 MPa .

Express your answer with appropriate units to three significant figures.

Hints

Pmax =
SubmitMy AnswersGive Up

Part B - Maximum length

A circular column with diameter 8.6 cm is to support a vertical load of 600 kN . What is the maximum length the column can have if it is pin supported at both ends? The material has E = 200 GPa . Assume the material does not yield.

Express your answer with appropriate units to three significant figures.

Hints

Lmax =
SubmitMy AnswersGive Up

Part C - Required diameter

A solid circular steel column with a height of 2.6 m needs to support a vertical load of 940 kN . What is the minimum diameter required if the factor of safety for buckling is FS = 2.5 and the material has E = 200 GPa? Assume the material does not yield.

Express your answer with appropriate units to three significant figures.

Hints

d =

Answer 1

A. Pmax = 588 KN

B. L = 2.97 m

C. d = 9.00 cm

Step-by-step explanation:

PART A:

First we calculate minimum moment of inertia:

Imin = (1/12)(base)(height)^3

Imin = (1/12)(0.096 m)(0.053 m)^3

Imin = 1.191 x
`10^(-6) m^(4)`

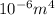
Now, for maximum load Pmax:

Pmax = π² E Imin/L²

Pmax = π²(200 x 10^9 N/m²)(1.191 x
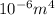`10^(-6) m^(4)`)/4 m²

Pmax = 588 KN

PART B:

I = (π/4)(r^4)

I = (π/4)(0.043 m)^4

I = 2.685 x
`10^(-6) m^(4)`

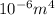
L² = π² E I/Pmax

L = √{π²(200 x 10^9 N/m²)(2.685 x
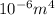`10^(-6) m^(4)`)/6 x 10^5 N}

L = 2.97 m

PART C:

Pmax = π² E I/L²

I = (Pmax)L²/π²E

I = (9.4 x 10^5 N)(2.6 m)²/π²(200 x 10^9)

I = 3.219 x
`10^(-6) m^(4)`

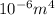
but,

I = (π/4)(r^4) = 3.219 x
`10^(-6) m^(4)`

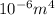
solving this,

r = 4.50 cm

and diameter will be:

d = 2r = 2(4.50 cm)

d = 9.00 cm