Question

There is a rectangle ABCD, with sides AB = CD = 32, and sides and BC = DA = 24. The rectangle is rotated 90° clockwise about C, then rotated 90° clockwise about the new location of point that D after the first rotation. What is the length of the path travelled by point A?

Answer 1

given,

side of rectangle, AB = CD = 32

BC = DA = 24

rectangle is rotated 90° clockwise about C.

then rotated 90° clockwise about D.

Path traveled by the point A for first rotation will be in circle with radius AC.

`D_1 = (\theta_1)/(360^0)* \pi * {AC}^2`

`AC = √(24^2+32^2)`

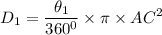
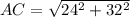
AC = 40

θ₁ = 90°

`D_1 = (90^0)/(360^0)* \pi * {40}^2`

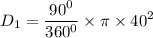
D₁ = 1256.64

For the second rotation Point A will move in circular path with radius of AD

`D_2 = (\theta_2)/(360^0)\pi {AD}^2`

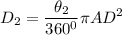
AD = 24

θ₁ = 90°

`D_2 = (90^0)/(360^0)* \pi * {24}^2`

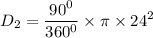
D₂ = 452.39

total path traveled by the point A

D = D₁ + D₂

D = 1256.64 + 452.39

D = 1709.03