Answer:
Δ
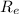 = 84 Ω,
= 84 Ω,
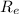 = (40 ± 8) 10¹ Ω
= (40 ± 8) 10¹ Ω
Step-by-step explanation:
The formula for parallel equivalent resistance is
1 /
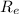 = ∑ 1 / Ri
= ∑ 1 / Ri
In our case we use a resistance of each
R₁ = 500 ± 50 Ω
R₂ = 2000 ± 5%
This percentage equals
0.05 = ΔR₂ / R₂
ΔR₂ = 0.05 R₂
ΔR₂ = 0.05 2000 = 100 Ω
We write the resistance
R₂ = 2000 ± 100 Ω
We apply the initial formula
1 /
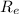 = 1 / R₁ + 1 / R₂
= 1 / R₁ + 1 / R₂
1 /
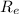 = 1/500 + 1/2000 = 0.0025
= 1/500 + 1/2000 = 0.0025
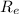 = 400 Ω
= 400 Ω
Let's look for the error (uncertainly) of Re
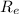 = R₁R₂ / (R₁ + R₂)
= R₁R₂ / (R₁ + R₂)
R’= R₁ + R₂
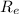 = R₁R₂ / R’
= R₁R₂ / R’
Let's look for the uncertainty of this equation
Δ
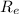 /
/
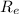 = ΔR₁ / R₁ + ΔR₂ / R₂ + ΔR’/ R’
= ΔR₁ / R₁ + ΔR₂ / R₂ + ΔR’/ R’
The uncertainty of a sum is
ΔR’= ΔR₁ + ΔR₂
We substitute the values
Δ
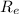 / 400 = 50/500 + 100/2000 + (50 +100) / (500 + 2000)
/ 400 = 50/500 + 100/2000 + (50 +100) / (500 + 2000)
Δ
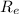 / 400 = 0.1 + 0.05 + 0.06
/ 400 = 0.1 + 0.05 + 0.06
Δ
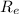 = 0.21 400
= 0.21 400
Δ
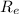 = 84 Ω
= 84 Ω
Let's write the resistance value with the correct significant figures
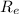 = (40 ± 8) 10¹ Ω
= (40 ± 8) 10¹ Ω