The distance between the foot of building to foot of ladder is 60 meters
Solution:
Given that A ladder, 100 m long reaches a point on the high-rise building that is 80 m above the ground
Given that ground is horizontal
The ladder, building and ground forms a right angled triangle
The figure is attached below
In the right angled triangle ABC,
AC represents the length of ladder
AC = 100 m
AB represents the height of building
AB = 80 m
BC represents the distance between the foot of building to foot of ladder
BC = ?
Pythagorean theorem, states that the square of the length of the hypotenuse is equal to the sum of squares of the lengths of other two sides of the right-angled triangle.
By above definition for right angled triangle ABC,
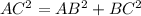
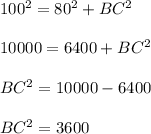
Taking square root on both sides,
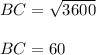
Thus the distance between the foot of building to foot of ladder is 60 meters