Question

The sum of the reciprocals of two consecutive integers is 9/20. Determine the consecutive integers algebraically.

I got the formula down, in the answer sheet it says the answers are 4 and 5.

Answer 1

The answer is 2 1/5.

Answer 2

Answer : The two consecutive integers are, 4 and 5

Step-by-step explanation :

Let the two consecutive number be, x and (x+1)

The sum of the reciprocals of two consecutive integers is 9/20.

The expression will be:

`(1)/(x)+(1)/(x+1)=(9)/(20)`

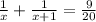
Now solving the term 'x', we get:

`(x+1+x)/((x)(x+1))=(9)/(20)`

`(2x+1)/(x^2+x)=(9)/(20)`

`20(2x+1)=9(x^2+x)`

`40x+20=9x^2+9x`

`9x^2-31x-20=0`

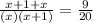
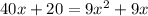
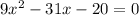
We are solving the quadratic equation by middle term splitting.

`9x^2-36x-5x-20=0`

`9x(x-4)+5(x-4)=0`

`(9x+5)(x-4)=0`

`(9x+5)=0\text{ and }(x-4)=0`

`x=(-5)/(9)\text{ and }x=4`

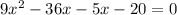
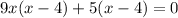
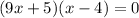
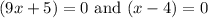
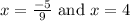
We are neglecting the value of
`x=(-5)/(9)`

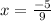
Thus we are taking x = 4

When x = 4 then (x+1) = (4+1) = 5

Thus, the two consecutive integers are, 4 and 5