Question

The maximum tension the wire can withstand without breaking is 300 N . A 0.800 kg projectile traveling horizontally hits and embeds itself in the wood ball. What is the largest speed this projectile can have without causing the cable to break?

Answer 1

Let's investigate the case where the cable breaks.

Conservation of angular momentum can be used to find the speed.

`\vec{L}_1 = \vec{L}_2\\\vec{L}_1 = m\vec{v_0} \\\vec{L}_2 = I\vec{\omega}\\`

The projectile embeds itself to the ball, so they can be treated as a combined object. The moment of inertia of the combined object is equal to the sum of the moment of inertia of both objects.

`I = I_(projectile) + I_(ball)\\I = mr^2 + mr^2\\I = 2mr^2`

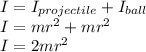
where r is the length of the cable.

After the collision, the ball and the projectile makes a circular motion because of the cable. So, the force (tension) in circular motion is

`F = (mv^2)/(r)`

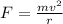
The relation between linear velocity and the angular velocity is

`v = \omega r`

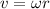
So,

`F = (m(\omega r)^2)/(r) = m\omega^2 r = 300\\mv_0r  =I\omega\\\\\omega = mv_0r/I\\300 = m((mv_0r)/(I))^2r = m((mv_0r)/(2mr^2))^2r = m((v_0)/(2r))^2r = (mv_0^2r)/(4r^2) = (mv_0^2)/(4r)\\300 = (0.8v_0^2)/(4r)\\1500 = v_0^2/r\\v_0 = √(1500r)`

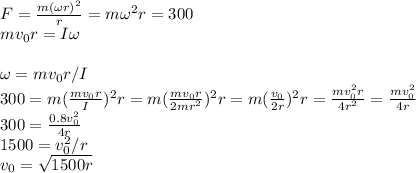
As can be seen, the maximum velocity for the projectile without breaking the cable is
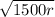`√(1500r)`, where r is the length of the cable.