Question

A 10-N object moves at 1 m/s. Its kinetic energy is __________.

A) 10 J.
B) 0.5 J.
C) 1 J.
D) more than 10 J.

Answer 1

To solve this problem we will first find the Mass of the Object given by Newton's second law and then apply the Kinetic Energy Theorem.

According to Newton's second law we have to

`F =ma \rightarrow m = (F)/(a)`

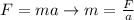
Where,

F = Force

m = mass

a = Acceleration, at this case is the same gravitational acceleration (
`9.8m/s^2`)

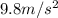Therefore the mass of the object is

`m = (F)/(g)`

`m = (10)/(9.8)`

`m = 1.0204kg`

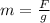
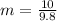
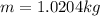
The cinematic energy theorem tells us that

`KE = (1)/(2) mv^2`

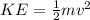
Where,

m = mass

v = Velocity

Replacing

`KE =(1)/(2) (1.0204)(1)^2`

`KE = 0.5102 \approx 0.5J`

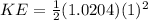
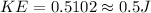
Therefore the correct answer is B.