Question

At 10:00 A.M., a car leaves a house at a rate of 60 mi/h. At the same time, another car leaves the same house at a rate of 50 mi/h in the opposite direction. At what time will the cars be 330 miles apart

Answer 1

The cars will be 330 miles apart after three hours (1.00 pm) from 10.00 am (starting time).

Explanation:

Data given for first car,

Rate (speed of car 1) = 60 miles/hour

Distance can be calculated by considering ‘X’ for time as,

`\text {rate}=\frac{\text {distance}}{\text {time}}`

`distance of first car = rate * time =60 * X miles`

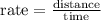
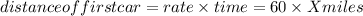
Similarly, data given for first car

Rate (speed of car 2) = 50 miles/hour

`distance of second car = rate * time =50 * X miles`

Need to calculate at what time both the cars are 330 miles apart, so the equation would be,

Distance of first car + distance of second car = 330 miles

60 X + 50 X = 330

110 X = 330

`X=(330)/(110)=3 \text { hours }`

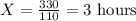
Already given that both the cars leave at 10.00 am, so the time would be 10 am + 3 hours = 1.00 pm.

Hence, it takes three hours for the cars to get 330 miles apart.