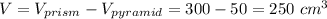Answer:
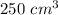
Explanation:
A rectangular prism has
- a height of 12 centimeters
- a square base with sides measuring 5 centimeters.
The volume of the prism is
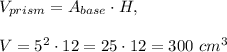
A pyramid with has
- the same base as the prism
- half the height of the prism
The volume of the pyramid is
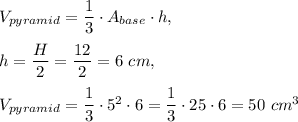
The volume of the space outside the pyramid but inside the prism is