Question

Show there is a number c ,with 0<_c<_1,such that f(c)=0 for the equation f(x)=x^3+x^2-1

Answer 1

Use Mean Value theorem.

Explanation:

Statement: If f(x) is continuous on [a, b] and differentiable on (a, b) then there is at least one 'c' (a < c < b), then we have:

f'(c) =
`$ (f(b) - f(a))/(b - a) $`

Here, f(x) = x³ + x² - 1. a = 0, b =1

Since, f(x) is a polynomial, it is continuous and differentiable on the interval.

f'(x) = 3x² + 2x

⇒ f'(c) = 3c² + 2c

Using Mean value theorem, we have:

3c² + 2c =
`$ (f(1) - f(0))/(1 - 0) $`

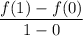
f(1) = 1 + 1 - 1 = 1

f(0) = 0 + 0 - 1 = - 1

`$ \implies f'(c) = (1 - (-1))/(1 - 0) $`

`$ \implies f'(c) = (2)/(1) = 2 $`

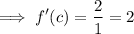
Therefore, we have: 3c² + 2c = 2

Rearranging this, we have: 3c² + 2c - 2 = 0 which is a quadratic equation.

Now, we find the roots of the equation using the formula:

We have: c =
`$ (- 2 \pm √(4 - 4(3)(2)))/(2.3) $`

=
`$ (- 2 \pm √(4 + 24))/(6) $`

=
`$ (- 2 \pm 2√(7))/(6) $`

=
`$ (- 1 \pm √(7))/(3) $`

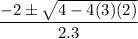
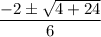
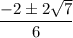
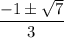
The roots are: c =
`$ (- 1 + √(7))/(6) , (- 1 - √(7))/(6) $`

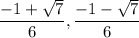
Since, our root should lie between 0 and 1, we eliminate
`$ (- 1 - √(7))/(6) $`.

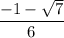Hence, the value of c =
`$ (- 1 + √(7))/(6) $`

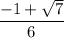
So, we have proved the existence of 'c' and have determined the value of 'c' as well.