Answer:
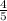
Explanation:
Given: There are 2 classes of 25 students.
13 play basketball
11 play baseball.
4 play neither of sports.
Lets assume basketball as "a" and baseball as "b".
We know, probablity dependent formula; P(a∪b)= P(a)+P(b)-p(a∩b)
As given total number of student is 25
Now, subtituting the values in the formula.
⇒P(a∪b)=
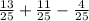
taking LCD as 25 to solve.
⇒P(a∪b)=
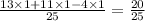
∴ P(a∪b)=
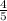
Hence, the probability that a student chosen randomly from the class plays both basketball and baseball is
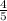 .
.