The only number that is not part of the solution set is 0 because it does not satisfy the inequality
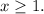 Option 1.
Option 1.
To determine which of the given numbers is not part of the solution set of the inequality
 we can solve the inequality step by step:
we can solve the inequality step by step:
1. We start with the given inequality:
![\[ x + 2 \geq 3 \]](https://img.qammunity.org/2021/formulas/mathematics/college/6vkk9bxhrstv6i0wx8tw93j82ksozw9ys1.png)
2. To isolate x on one side of the inequality, we subtract 2 from both sides:
![\[ x + 2 - 2 \geq 3 - 2 \]](https://img.qammunity.org/2021/formulas/mathematics/college/m8zrcvhvnyfzbijsnn0nirrrvi41g81w6n.png)
![\[ x \geq 1 \]](https://img.qammunity.org/2021/formulas/mathematics/college/8532o42ur2dadi2nvwobmqurtzghmzqqj0.png)
This means that any number greater than or equal to 1 is part of the solution set of the inequality.
3. Now, we look at the given options to determine which one is not a solution:
- 0 is less than 1, so 0 is not part of the solution set.
- 2 is greater than 1, so 2 is part of the solution set.
- 3 is greater than 1, so 3 is part of the solution set.
- 6 is greater than 1, so 6 is part of the solution set.