Answer:
The Proof is given below.
Explanation:
Given:
P is the center of Circle
∠ONE ≅ ∠TEN
To Prove:
∠5 ≅ ∠6
Proof:
Exterior Angle Theorem:
Exterior Angle Property of a Triangle states that measure of exterior angle of a triangle is equals to the sum of measures of its interior opposite angles.
STATEMENT REASON
1. So In ΔONE,
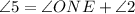 1. Exterior Angle Property of a Triangle.
1. Exterior Angle Property of a Triangle.
2. Similarly In ΔTEN,
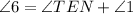 2. Exterior Angle Property of a Triangle.
2. Exterior Angle Property of a Triangle.
3. But , ∠ONE ≅ ∠TEN 3. Given
4. And P is the center of circle So
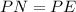 4.radius of same circle
4.radius of same circle
5. ΔPEN is an Isosceles triangle,
∴ ∠ 1 ≅ ∠ 2 5. Isosceles triangle property
6. ∴ ∠5 ≅ ∠6 6. From 3 and 5 Transitive Property.........Proved