Answer:
i. The slope of the equation is -2.
ii. The y-intercept of the equation is 6.
Explanation:
Hey there!
First, let's find the slope using the slope formula:
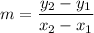
We are given the points in the form (x₁, y₁), (x₂, y₂), which means we can define our values for these coordinates:
Then, we can plug these into the slope formula:
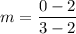
Now, let's simplify the fraction by evaluating the numerator and the denominator separately.
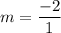
Finally, we can simplify this to a whole number since we are dividing by 1.

Now, we can find the y-intercept of the line using the point-slope equation:
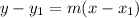
Plug in the known values:
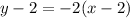
Simplify by using the distributive property:
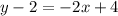
Add 2 to both sides:
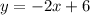
This gives us the equation of the line in slope-intercept form, which means we can extract the y-intercept from this equation.
The base equation for slope-intercept form is:
 ,
,
where b is the y-intercept.
Therefore, the y-intercept of the equation is 6 and the slope of the equation is -2.