Question

More math question please help!!
Answer all correctly

Answer 1

See below for answers and explanations

Explanation:

Problem 1

To multiply two complex numbers in polar form, we use the rule
`z_1z_2=r_1r_2[cos(\theta_1+\theta_2)+isin(\theta_1+\theta_2)]`, so:

`z_1z_2=r_1r_2[cos(\theta_1+\theta_2)+isin(\theta_1+\theta_2)]\\z_1z_2=(2)(8)[cos(60^\circ+150^\circ)+isin(60^\circ+150^\circ)]\\z_1z_2=16(cos210^\circ+isin210^\circ)`

This means that C is the correct answer

Problem 2

We treat a complex plane almost exactly like a Cartesian plane where the x-axis is the real axis and the y-axis is the imaginary axis. Hence, point A is located at (3,-5) if this were a Cartesian plane, but since it is a complex plane, it would be read as 3-5i, making A the correct answer

Problem 3

The first part of the problem is really just using the distance formula, treating the real and imaginary parts of the complex numbers as coordinate points:

`√((6-2)^2+(7-(-5))^2)\\√((4)^2+(7+5)^2)\\√(16+(12)^2)\\√(16+144)\\√(160)\\4√(10)`

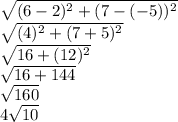
The second part of the problem is simple enough, again, treating the real and imaginary parts of the complex numbers as coordinate points:

`\bigr((2+6)/(2),(-5+7)/(2)\bigr)=\bigr((8)/(2),(2)/(2)\bigr)=(4,1)=4+i`

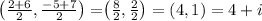
Thus, A is the correct answer

Problem 4

Rectangular Form:
`z=a+bi`

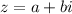
Polar/Trigonometric Form:
`z=r(cos\theta+isin\theta)`

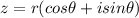
Conversion Rules:
`r=√(a^2+b^2)\\\theta=tan^(-1)((b)/(a))`

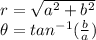
Calculations:

`r=\sqrt{(-5√(3))^2+(-5)^2}\\r=√(75+25)\\r=√(100)\\r=10`

`\theta=tan^(-1)((-5)/(-5√(3)))\\\theta=tan^(-1)((1)/(√(3)))\\\theta=30^\circ`

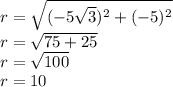
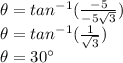
Because the complex number is located in Quadrant III, then the reference angle is
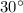`30^\circ` counterclockwise from the negative x-axis, which is equal to
`180^\circ+30^\circ=210^\circ`

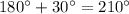
Thus, the complex number is trigonometric form is
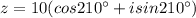`z=10(cos210^\circ+isin210^\circ)`, making C the correct answer

Problem 5

This is just a simple evaluation:

`6\biggr(cos(5\pi)/(6)+isin(5\pi)/(6)\biggr)\\ \\6\biggr(-(√(3))/(2)+(1)/(2)i\biggr)\\ \\-3√(3)+3i`

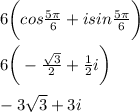
Treating the real and imaginary parts of the complex number as coordinate points, we can see that the best point is Q.

Answer 2

Explanation:

Complex numbers polar multiplication form:

`\boxed{z_(1)z_(2)=r_(1)*r_(2)(Cos \ (\theta_(1)+ \theta_(2))+iSin \ (\theta_(1)+ \theta_(2))}`

z₁ = 2 (Cos 60 + i Sin 60) & z₂ = 8(Cos 150 + i Sin 150)

z₁z₂= 2*8 (Cos [60+150] + i Sin [60+150])

= 16 (Cos 210 + i Sin 210) Option C

2) Point A : 3 - 5i Option A

The x-axis represent real part and the y-axis represent imaginary part.

4) z = -5√3 -i 5

x = -5√3 & y = -5

`r=\sqrt{x^(2)+y^(2)}\\\\ = \sqrt{(-5√(3))^(2)+(-5)^(2)}\\\\ = √(25*3 + 25)= √(75+25)\\\\ = √(100)\\\\r = 10`

`\theta = tan^(-1) \ (y)/(x)\\\\\\=tan^(-1) \ (-5)/(-5√(3))\\\\\\= tan^(-1) \ (1)/(√(3))`

`\sf \theta = 30^ \circ`

Theta lies in third quadrant

Ф = 180 + 30

Ф = 210°

z = 10(Cos 210° + i sin 210°)