Answer:
5.4 ms⁻¹
Step-by-step explanation:
Here we have to use conservation of energy. Initially when the stick is held vertical, its center of mass is at some height above the ground, hence the stick has some gravitational potential energy. As the stick is allowed to fall, its rotates about one. gravitational potential energy of the stick gets converted into rotational kinetic energy.
 = length of the meter stick = 1 m
= length of the meter stick = 1 m
 = mass of the meter stick
= mass of the meter stick
 = angular speed of the meter stick as it hits the floor
= angular speed of the meter stick as it hits the floor
 = speed of the other end of the stick
= speed of the other end of the stick
we know that, linear speed and angular speed are related as
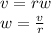
 = height of center of mass of meter stick above the floor =
= height of center of mass of meter stick above the floor =
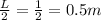
 = Moment of inertia of the stick about one end
= Moment of inertia of the stick about one end
For a stick, momentof inertia about one end has the formula as
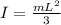
Using conservation of energy
Rotational kinetic energy of the stick = gravitational potential energy
