Question

Pleaseeee helppp!!!

Just the first question.
1.)
Brenda decides to save her spare change in a jar. The initial amount in the jar, J(0). is $20, and after one week it is (7) = 23.50.

Answer 1

(a) Brenda saved $23.50.

(b) The rate at which Brenda is saving money is 0.5 dollars per day.

(c) money saved on
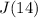`J(14)` is $27.

Explanation:

Given:

Initial amount in the jar is,
`J(0)=\$20`

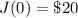
Amount in the jar after a week or 7 days is,
`J(7)=\$23.50`

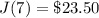
Brenda is saving money at a linear rate.

(a)

Now, money at the end of the week is the total money saved by Brenda.

Therefore, total money saved by Brenda is equal to the money saved at the end of the week. So,

Total money saved by Brenda =
`J(7)=\$23.50`

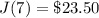
(b)

The rate of change of a function is given as:

`Rate=(f(x_2)-f(x_1))/(x_2-x_1)`

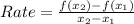
Here,
`x_1=0,x_2=7, f(x_1)=J(0),f(x_2)=J(7)`

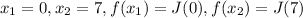
Therefore, the rate at which Brenda saves money is given as:

`Rate=(J(7)-J(0))/(7-0)\\Rate=(23.50-20)/(7)\\Rate=(3.5)/(7)=0.5\ dollars/day`

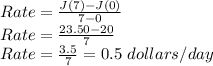
Therefore, the rate at which Brenda is saving money is 0.5 dollars per day.

(c)

A linear function is of the form
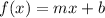`f(x)=mx+b`, where 'm' is the rate and 'b' is the initial value of the function.

Therefore, the linear function for the money saved by Brenda can be written as:

`J(x)=(Rate)x+J(0)\\J(x)=0.5x+20`

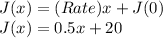
Now,
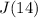`J(14)` is given by plugging in 14 for 'x' in the above expression. So,

`J(14)=0.5* 14+20\\J(14)=7+20=\$27`

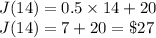
Therefore, money saved on
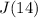`J(14)` is $27.