Question

WORTH 15 POINTS PLEASE ANSWER ASAP!! MY YOUNGER BROTHER NEEDS HELP ON THIS!!!!
∧ω∧

Answer 1

what she said lol

Answer 2

Therefore,

AD = 7 unit

AE = 600 unit

EF = 30 unit

FB = 5 unit

Ar(EFGH)= 210 unit²

Ar(ABCD)= 4445 unit²

Explanation:

Given:

Consider a rectangle ABCD as shown in the figure below where,

Area (ABCD) = 635 × 7 = 4445

Therefore length and width of a rectangle will be

LENGTH =635 = AB

WIDTH = 7 = AD

To Find:

AE =?

EF = ?

FB = ?

Ar(EFGH)=?

Ar(ABCD) =?

Solution:

We know that area of the rectangle is given by

`\textrm{Area of rectangle}= LENGTH* WIDTH`

`\textrm{Area of rectangle ABCD}= 635* 7=4445\ unit^(2)`

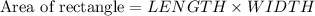
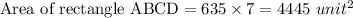
Substituting the values we get

`\textrm{Area of rectangle AEHD}= AE* 7\\\\4200=AE* 7\\\therefore AE=(4200)/(7)=600`

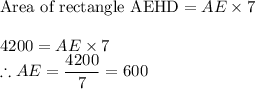
Similarly for area rectangle FBCG,

`\textrm{Area of rectangle FBCG}= FB* 7\\\\35=FB* 7\\\therefore FB=(35)/(7)=5`

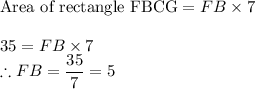
Now we have

AB = 635,

`AE + EF + FB = 635\\\\600+EF+5=635\\\\EF=635 -605=30\\\therefore EF = 30`

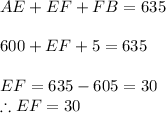
Similarly for area rectangle EFGH,

`\textrm{Area of rectangle EFGH}= EF* 7\\\\=30* 7=210\ isunit^(2)`

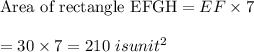
Therefore,

AD = 7 unit

AE = 600 unit

EF = 30 unit

FB = 5 unit

Ar(EFGH)= 210 unit²

Ar(ABCD)= 4445 unit²