Question

How to solve -16x+2y=-2, y=8x-1 by using substitution

Answer 1

For this case we have the following system of equations:

`-16x + 2y = -2\\y = 8x-1`

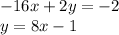
To solve, we substitute the second equation in the first:

`-16x + 2 (8x-1) = - 2`

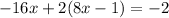
We apply distributive property to the terms within parentheses:

`-16x + 16x-2 = -2\\-2 = -2`

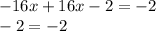
Equality is met, so for any value of x it will be fulfilled. Therefore, the system of equations has infinite solutions.

Answer:

Infinite solutions