Question

Prove there exists a positive number c such that two inner products with corresponding norms?

Answer 1

See explanation below

Explanation:

We assume that we have two inner products
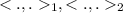`<.,.>_1,<.,.>_2` on v such that
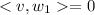`<v,w_1>=0` if and only if
`<v,w>_2 =0` and we want to proof is there is a positive number c like this :

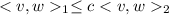`<v,w>_1 \leq c<v,w>_2` for every
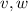`v,w` in V

We can assumee that we have an orthonormal basis
`{v_1,....,v_n}` of V with respect
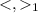`<,>_1`. We can define the following sets:

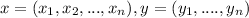`x= (x_1, x_2,...,x_n), y=(y_1 ,....,y_n)` both defined on a n dimensional space, and then we have that for any linear comibnation we have this:

`<\sum_(i=1)^n x_i v_i, \sum_(k=1)^n y_k v_k>_2 = x'Ax`

And A neds to be a matrix with entries
`a_(ij)= <v_i, v_j>`

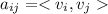
So then we have this:

`r(x) = (||x||_2)/(||x||_1) =(x' A x)/(x' x)`

And then we have the maximum defined and we need to satisfy that c is the maximum value for te condition required.

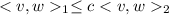`<v,w>_1 \leq c<v,w>_2` for every
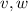`v,w` in V