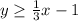Answer:
Option B.
Explanation:
A solid straight line passes through (0, -1) and (3, 0)
Slope of the line =
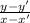
=
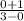
=

Equation of the line passing through (0, -1) will be
y - y' = m(x - x')
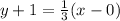
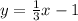
Since this line is solid then there will the sign of (≥ or ≤)
If everything above and to the left of the line is shaded then the inequality will be
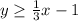
Therefore, the answer will be option B.