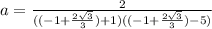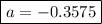Question

An isosceles trapezoid ABCD with height 2 units has all its vertices on the parabola y=a(x+1)(x−5). What is the value of a, if points A and D belong to the x−axis and m∠BAD=60^o?

Answer 1

a = -0.3575

Explanation:

The points A and D lie on the x-axis, this means that they are the x-intercepts of the parabola, and therefore we can find their location.

The points A and B are located where

`y=a(x+1)(x-5)=0`

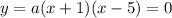
This gives

`x=-1`

`y=5`

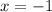
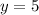
Now given the coordinates of A, we are in position to find the coordinates of the point B. Point B must have y coordinate of y=2 (because the base of the trapezoid is at y=0), and the x coordinate of B, looking at the figure, must be x coordinate of A plus horizontal distance between A and B, i.e

`B_x=A_x+(2)/(tan(60)) =-1+(2√(3) )/(3)`

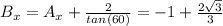
Thus the coordinates of B are:

`B=(-1+(2√(3) )/(3),2)`

Now this point B lies on the parabola, and therefore it must satisfy the equation
`y=a(x+1)(x-5).`

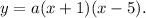
Thus

`2=a((-1+(2√(3) )/(3))+1)((-1+(2√(3) )/(3))-5)`

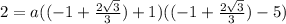
Therefore

`a=(2)/(((-1+(2√(3) )/(3))+1)((-1+(2√(3) )/(3))-5))`

`\boxed{a=-0.3575}`