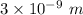Question

What is the mechanical work done by the initial load placed on a fiber if the fiber is linearly deformed by 3 nm?

Answer 1

`W=4.5\ k* 10^(-18)\ J`

Step-by-step explanation:

The mechanical work done by the load placed on a fiber if the fiber deforms by 3 nano-meter can be given in relation to the energy stored in a stretched fiber.

• We know according to the Hooke's law within the elastic limit the stress is directly proportional to the strain. The constant introduced is called stiffness constant defined as the magnitude of load applied for the deformation of one unit in the dimension of the object.

The energy stored in a stretched fiber is equal to the work done:

`W=(1)/(2) k.\Delta x^2`

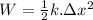
where:

k = stiffness constant

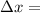`\Delta x=` deformation in the fiber =
`3* 10^(-9)\ m`

`W=4.5\ k* 10^(-18)\ J`