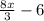Question

The length of a rectangle is 3 units shorter than one-third of the width, x.

Which expression represents the perimeter of the rectangle?

8/3x−6
2/3x−4
8/3x−2
Why is that correct?
2/3x−8

Answer 1

`(8x)/(3) - 6` is the expression that represents the perimeter of rectangle

Solution:

Let "x" represent the width of rectangle

Given that length of rectangle is 3 units shorter than one-third of the width x

length of rectangle = one-third of the width x - 3

`\text{ length of rectangle} = (1)/(3)x - 3 = (x)/(3) - 3\\\\\text{ length of rectangle} = (x)/(3) - 3`

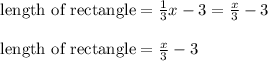
The perimeter of rectangle is given as:

perimeter of rectangle = 2(length + width)

Substituting the known values we get,

`\text{ perimeter of rectangle }= 2((x)/(3) - 3 + x)\\\\\rightarrow 2((x - 9 + 3x)/(3))\\\\\rightarrow 2((4x-9)/(3))\\\\\rightarrow(8x-18)/(3)\\\\\rightarrow(8x)/(3) - (18)/(3)\\\\\rightarrow(8x)/(3) - 6`

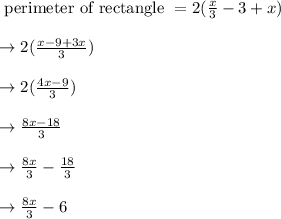
Thus perimeter of rectangle is
`(8x)/(3) - 6`

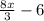
Thus option 1 is correct