Answer:
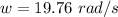
Step-by-step explanation:
Circular Motion
Suppose there is an object describing a circle of radius r around a fixed point. If the relation between the angle of rotation by the time taken is constant, then the angular speed is also constant. If that relation increases or decreases at a constant rate, the angular speed is given by:
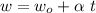
Where
 is the angular acceleration and t is the time. If the object was instantly released from the circular path, it would have a tangent speed of:
is the angular acceleration and t is the time. If the object was instantly released from the circular path, it would have a tangent speed of:
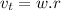
We have two reels: one loaded with the tape to play and the other one empty and starting to fill with tape. They both rotate at different angular speeds, one is increasing and the other is decreasing as the tape goes from one to the other. We'll assume the tangent speed is constant for both (so the tape can play correctly). Let's call
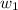 the angular speed of the loaded reel and
the angular speed of the loaded reel and
 that from the empty reel. We have
that from the empty reel. We have
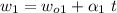
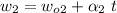
If
 is the radius of the reel when it's full of tape, the angular speed for the loaded reel is computed by
is the radius of the reel when it's full of tape, the angular speed for the loaded reel is computed by
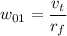
The tangent speed is computed by knowing the length of the tape and the time needed to fully play it.
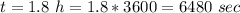
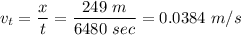
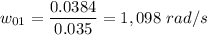
If
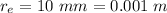 is the radius of the reel when it's empty, the angular speed for the empty reel is computed by
is the radius of the reel when it's empty, the angular speed for the empty reel is computed by

The full reel goes from
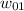 to
to
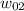 in 6480 seconds, so we can compute the angular acceleration:
in 6480 seconds, so we can compute the angular acceleration:
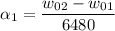
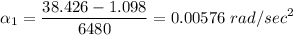
The empty reel goes from
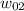 to
to
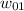 in 6480 seconds, so we can compute the angular acceleration:
in 6480 seconds, so we can compute the angular acceleration:

So the equations for both reels are
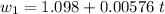

They will be the same when
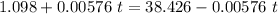
Solving for t
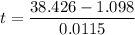
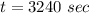
The common angular speed is
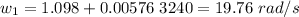

They both result in the same, as expected
