Answer:
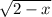 is the final answer
is the final answer
Explanation:
If each expression under the square root is greater than or equal to 0, what is x2−6x+9−−−−−−−−−√+2−x−−−−√+x−3x2−6x+9+2−x+x−3?
can be rearranged as thus
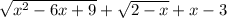
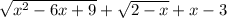 factorizing x^2-6x+9
factorizing x^2-6x+9
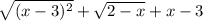 ..................1
..................1
take note that
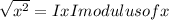
Ix-3I+
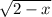 ...................2
...................2
Ix-3I is equal to -(x-3)...............3
Now, as the expressions under the square roots are greater than or equal to zero than 2−x≥0
2−x≥0
--> -x≤-2
x≤2.
substituting 3 into the equation 2
-(x-3)+
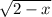 +x-3
+x-3
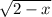 is the final answer
is the final answer