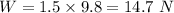Question

You have landed on an unknown planet, Newtonia, and want to know what objects weigh there. When you push a certain tool, starting from rest, on a frictionless horizontal surface with a 12.0-N force, the tool moves 16.0 m in the first 2.00 s. You next observe that if you release this tool from rest at 10.0 m above the ground, it takes 2.58 s to reach the ground. What does the tool weigh on Newtonia, and what does it weigh on Earth?

Answer 1

Step-by-step explanation:

Given

Force applied
`F=12\ N`

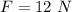
time taken
`t_1=2\ s`

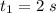
Displacement
`s=16\ m`

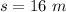
using

`s=ut+(1)/(2)at^2`

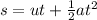
u=initial velocity

s=displacement

t=time

`16=0+(1)/(2)a(2)^2`

`a=8\ m/s^2`

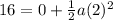
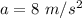
thus mass of body
`m=(F)/(a)=(12)/(8)=1.5\ kg`

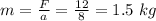
Next it is released from a height of
`h=10\ m`

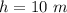
time taken to reach ground
`t_2=2.58\ s`

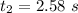
using
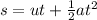`s=ut+(1)/(2)at^2` in vertical direction

here acceleration is due to acceleration due to gravity(g') of the planet

as it at rest so u=0 here

`10=0+(1)/(2)(g')(2.58)^2`

`g'=3.004\ m/s^2`

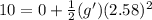
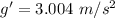
Thus acceleration due to gravity on Newtonian is
`3\ m/s^2`

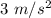
Weight of tool on Newtonia
`W'=mg'`

`W'=1.5* 3.004=4.506\ N`

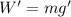
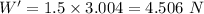
Weight on Earth
`W=1.5* 9.8=14.7\ N`