Question

A boat traveled 147 miles downstream and back. The trip downstream took 7 hours. The trip back took 21 hours. What is the speed of the boat In still water? What is the speed of the current?

Answer 1

The speed of current is 7 miles per hour

Explanation:

Given as :

The distance cover by boat in downstream = D = 147 miles

The distance cover by boat in upstream = d = 147 miles

The time taken in downstream trip = T = 7 hours

The time taken in upstream trip = t = 21 hours

Let The speed of boat in still water = x mi/h

And The speed of current = y mi/h

The speed in downstream = S = (x + y) mi/h

The speed in upstream = s = (x - y) mi/h

Now, According to question

∵ Distance = speed × time

For downstream

D = S × T

Or, 147 miles = (x + y) mi/h × 7 hours

i.e 7 (x + y) = 147

Or, x + y =
`(147)/(7)`

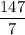
∴ x + y = 21 ........A

For upstream

d = s × t

Or, 147 miles = (x - y) mi/h × 21 hours

i.e 21 (x - y) = 147

Or, x - y =
`(147)/(21)`

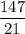
∴ x - y = 7 .......B

Now, Solving equations A and B

So, (x + y) + (x - y) = 21 + 7

Or, (x + x) + (y - y) = 28

Or, 2 x + 0 = 28

∴ x =
`(28)/(2)`

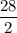
i.e x = 14 miles per hour

The speed of boat in still water = x = 14 mi/h

Now, putting the value of x into eq B

So, y = x - 7

Or, y = 14 - 7

i.e y = 7 miles per hour

The speed of current = y = 7 mi/h

Hence, The speed of current is 7 miles per hour . Answer