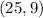Question

Can someone solve this? i have a photo.

Answer 1

Answer:
`(25,9)`

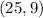
Explanation:

In order to write an equivalent equation for the first equation, you can multiply both sides by 15:

`(15)((x)/(5)+(y)/(3))=(8)(15)\\\\3x+5y=120`

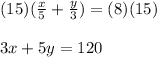
Then, you get this system of equations:

`\left \{ {{3x+5y=120} \atop {x-2y=7}} \right.`

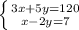
Now, you can apply the Elimination Method to solve the system of equations:

1. Multiply the second equation byb -3.

2. Add the equations.

3. Solve for "y".

Then:

`\left \{ {{3x+5y=120} \atop {-3x+6y=-21}} \right.\\.....................\\11y=99\\\\y=9`

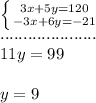
4. Substitute the value of "y" into any original equation and solve for "x" in order to find its value:

`x-2(9)=7\\\\x=7+18\\\\x=25`

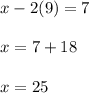
5. The solution is:

`(25,9)`