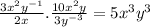Question

Simplify the expression

3x^2y^-1/2x • 10x^2y/3y^-3

*these two are fractions being multiplied if you are confused*

Answer 1

The simplified given expression
`(3x^2y^(-1))/(2x).(10x^2y)/(3y^(-3))` is
`5x^3y^3`

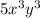
Explanation:

Given expression is

`(3x^2y^(-1))/(2x).(10x^2y)/(3y^(-3))`

To find the simplified expression:

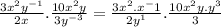`(3x^2y^(-1))/(2x).(10x^2y)/(3y^(-3))=(3x^2.x^-1)/(2y^1).(10x^2y.y^3)/(3)` ( Using the properties
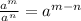`(a^m)/(a^n)=a^(m-n)` and
`a^m.a^n=a^(m+n)` )

`=(3x^(2-1))/(2y).(10x^2y^(1+3))/(3)`

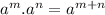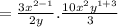
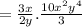`=(3x)/(2y).(10x^2y^4)/(3)` (using division property to the terms)

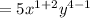`=5x^(1+2)y^(4-1)` ( Using the properties
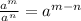`(a^m)/(a^n)=a^(m-n)` and
`a^m.a^n=a^(m+n)` )

`=5x^3y^3`

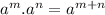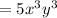
Therefore
`(3x^2y^(-1))/(2x).(10x^2y)/(3y^(-3))=5x^3y^3`

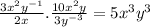
Therefore the simplified given expression is
`5x^3y^3`

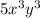
Therefore simplified expression is given by
`(3x^2y^(-1))/(2x).(10x^2y)/(3y^(-3))=5x^3y^3`