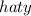Question

If n = p + 1, and the X matrix is invertible, show that the hat matrix H is given by the (p + 1) ∗ (p + 1) identity matrix. In this case, what are hii and yˆi?

Answer 1

Explanation:

Consider that we have a multiple linear model given by this:

`y = \beta X + e`

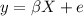
And we assume that we have p independent variables and p+1 is the dimension with the vector including the intercept, so then n =p+1.

For this case we want to minimize the sum of error
`\sum_(i=1)^n e^2_i`

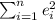
And we have this:

`min e'e = (y-Xb)' (y-Xb)`

`min e'e= y'y -2b'X'y +b'X'Xb`

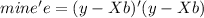
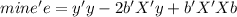
And when we find the partial derivate respect to b we got:

`(d(e'e))/(db) =-2X'y + 2X'Xb =0`

`X'X b= X' y`

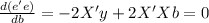
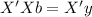
We are assuming that the matrix X is invertible(non singular). And applying the inverse matrix X'X on both sides we got:

`b =\hat \beta =(X'X)^(-1) X'y`

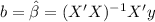
The estimator for [tex\beta[/tex] is given by:

`\hat \beta = (X^T X)^(-1) X^T y`

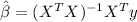
And the predicted values can be written like this:

`\hat y = X \hat \beta =[X(X^T X)^(-1) X^T]= Hy`

And we can see that
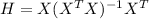`H=X(X^T X)^(-1) X^T` and on this case if we find the dimensions for H, assuming that X is nxn. Then H is a matrix nxn since only depends of the matrix X.

On this case the elements
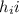`h_ii` represent the elements of the diagonal for the matrix H and are used in order to find the estimated values
`hat y`